‘Wetenschappelijk bewezen’ wat is dat eigenlijk? Deel 1 van een drieluik
Inleiding
Termen als wetenschappelijk bewezen of wetenschappelijk onderbouwd worden te pas en te onpas gebruikt. Merken als Becel1Uitleg over margarines door Becel. Geraadpleegd 11 oktober 2015, supplementenverkopers2Site voor magnesiumsupplementen. Geraadpleegd 11 oktober 2015, het Voedingscentrum3Over het Voedingscentrum. Geraadpleegd 11 oktober 2015 en ook politici en bewindslieden4Videoboodschap van Minister Schippers (VWS). Geraadpleegd 11 oktober 2015 bedienen zich ervan om hun claims of beleid kracht bij te zetten. Maar wie kan vertellen wat ze bedoelen als ze die termen gebruiken? Ook journalisten, beleidsmakers, rechters en zelfs wetenschappers5Theocharis, T., & Psimopoulos, M. (1987). Where science has gone wrong. Nature, 329(6140), 595–598 hebben moeite met die vraag. Toch is een antwoord wel te geven, want sinds het ontstaan van de wetenschappelijke aanpak zo’n 2400 jaar geleden, hebben tal van filosofen, wetenschappers en andere denkers zich gebogen over de vraag wanneer we kunnen stellen dat iets wetenschappelijk waar is.
Om iets te kunnen zeggen over de betekenis van de termen, moet de vraag worden beantwoord: wat zijn wetenschappelijke bevindingen? Het antwoord op die vraag is niet, zoals wel eens gedacht wordt, bevindingen die door wetenschappers zijn gedaan5. Nee, het moet worden gezocht worden in de manier waarop die bevindingen tot stand zijn gekomen.
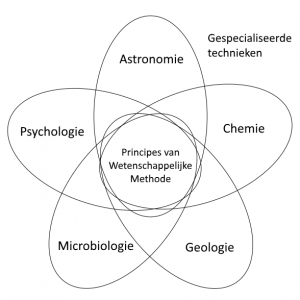
Wetenschappelijk onderzoek maakt gebruik van specialistische technieken en algemene principes. De laatste zijn samen te vatten onder de noemer wetenschappelijke methode. Naar: 6Gauch, H. G. (2003). Scientific method in practice. New York: Cambridge University Press.
Daar is niet één manier voor – een bioloog gaat bijvoorbeeld anders te werk dan een astronoom – maar wel wordt er telkens gebruik gemaakt van enkele basisprincipes, samen te vatten onder de term wetenschappelijke methode, zoals weergegeven in de illustratie.
Het doel van dit eerste artikel van een drieluik is om deze principes te bespreken om daarmee te laten zien wat wetenschappelijk bewezen inhoudt. In het tweede deel beschrijf ik wat dit betekent voor onze kennis over voeding en de stellingen van bijvoorbeeld het Voedingscentrum, boekenschrijvers, of voedingsproducenten. In het derde deel onderzoek ik of er mogelijkheden zijn om overtuigender conclusies te trekken bij voedingsonderzoek.
Het PEL-model van wetenschappelijke methode
Veel teksten in boeken en lesmateriaal over de principes van de wetenschappelijke methode beschrijven die als een soort geordend stappenplan. Het is dan ook niet verwonderlijk dat wikipedia de methode zo definieert7Empirische cyclus – Wikipedia. Geraadpleegd 11 oktober 2015.. In praktijk worden de diverse basisprincipes echter door elkaar heen gebruikt6, zoals ook de AAAS – de grootste Amerikaanse organisatie voor wetenschap en uitgever van het blad Science – beschrijft8Project 2061 (American Association for the Advancement of Science). (2000). Designs for science literacy, proloog. New York: Oxford University Press. Geraadpleegd 11 oktober 2015.:
“science … which is often misrepresented as a fixed sequence of steps … is a highly variable and creative process. Nevertheless, … it has certain features that show up again and again.”
Er is dus geen algemeen toepasbaar recept om tot wetenschappelijke bevindingen te komen, maar ze voldoen wel wel aan telkens terugkerende algemene principes. Deze principes vormen de kern van de wetenschap en begrip ervan is de sleutel tot het antwoord op de vraag wat wetenschappelijk mag heten. De telkens terugkerende principes worden goed beschreven met het zogenaamde PEL-model6, wat staat voor presuppositions, evidence, en logic (vooronderstellingen, aanwijzingen en logica).
Vooronderstellingen
De eerste van de drie componenten van het PEL-model – vooronderstellingen – lijkt volledig in strijd met de objectiviteit die wetenschap zegt te bieden. Toch is het een essentieel en onvermijdelijk onderdeel van wetenschap. Wat zijn vooronderstellingen precies? In feite zijn dit onderliggende dingen waarvan (meestal onuitgesproken) wordt aangenomen dat ze waar zijn. Een meer precieze definitie is: de vooronderstellingen van een vraag zijn dingen die waar moeten zijn wil de vraag een antwoord hebben6,9Khatchadourian, H. (1955). Some Metaphysical Presuppositions of Science. Philosophy of Science, 22(3), 194–204..
Zo doen wetenschappers de metafysische vooronderstelling dat de fysische wereld bestaat. Dit lijkt triviaal, maar dat is wel precies het punt waarvan sceptici (een stroming binnen de filosofie) stellen dat we dit niet kunnen weten en dat wetenschap daarom geen absolute kennis kan opleveren. Daarnaast veronderstellen wetenschappers doorgaans dat dingen in de wereld zich volgens consistente patronen gedragen, en dat we deze patronen door middel van nauwkeurige, systematisch onderzoek kunnen begrijpen10Rutherford, F. J., & Ahlgren, A. (1990). Science for all Americans, chapter 1. New York: Oxford University Press. Geraadpleegd 11 oktober 2015. We moeten deze drie veronderstellingen – die onmogelijk aangetoond kunnen worden – doen omdat wetenschap anders geen betekenis heeft. Wie vraagt waarom deze zaken dan voor waar worden aangenomen, krijgt als antwoord dat common sense – gezond verstand – dit nu eenmaal voorschrijft. Dit soort vooronderstellingen doen we allemaal. Niemand gaat er bijvoorbeeld vanuit dat het beeldscherm waarop je dit nu leest ineens gewichtsloos wordt en wegvliegt.
Naast deze algemene aannames worden bij elk onderzoek ook specifieke vooronderstellingen gedaan. Dit kan zich al uiten in de onderzoeksvraag. Stel dat die luidt: worden muizen dik van vet of van koolhydraten? Dan zitten in de vraag al de vooronderstellingen dat muizen niet dik worden van vet en koolhydraten, noch van een onbenoemde derde factor. Het is dus belangrijk om een onderzoeksvraag goed te formuleren. Veelal bouwen dit soort specifieke vooronderstellingen voort op eerdere onderzoeksresultaten. Bekende voorbeelden binnen de voedingswetenschap zijn de vooronderstellingen dat verzadigd vet ongezond is, dat veel zout de bloeddruk verhoogt, of dat het zinvol is om voeding in te delen naar het aandeel macronutriënten. De eerste twee komen bijvoorbeeld tot uiting in de definitie van een ‘ongezond’ voedingspatroon. Dit type vooronderstellingen is gebaseerd op een zekere hoeveelheid bestaande evidence en logica. Desondanks blijven het wel vooronderstellingen en zal soms blijken dat die onderliggende evidence ook anders geïnterpreteerd kan worden.
Het essentiële punt is dat als de vooronderstellingen onduidelijk zijn, het concept van evidence ook niet helder is. Twijfels over conclusies, of meningsverschillen over de betekenis van observaties hebben vaak hun oorsprong in een verschil in vooronderstellingen. Een discussie over wetenschappelijke conclusies heeft daarom alleen maar zin als alle deelnemers hun vooronderstellingen kenbaar maken. Bovendien is die dialoog interessant omdat daaruit het denkkader achter het onderzoek duidelijk wordt en het getoetst kan worden aan onderzoeksresultaten vanuit andere denkkaders.
Aanwijzingen
De tweede pijler van het PEL-model is evidence. Vaak wordt dit vertaald als bewijs, maar dat is onjuist. Het woord bewijs suggereert namelijk dat iets volkomen vast staat. De term evidence gaat echter over verkregen data, over gegevens die iets zeggen over de geteste hypothese, namelijk dat die al dan niet plausibel is. De evidence laat zien of het denkkader consistent is met praktijktests Een betere vertaling is daarom: aanwijzingen.
Evidence – meting of observatie – speelt een essentiële rol binnen het wetenschappelijk proces. Niet alle gegevens kunnen echter worden gebruikt, ze moet tenminste aan twee regels voldoen6. Ten eerste moeten de data toelaatbaar zijn ten aanzien van de vooronderstellingen. Dat betekent bijvoorbeeld dat data geen (voorspellende) waarde heeft als wordt afgezien van de bovengenoemde vooronderstelling dat dingen in consistente patronen gebeuren. Ten tweede moeten de gegevens relevant zijn voor de hypotheses die worden getoetst. Bijvoorbeeld, om te bepalen of hypothese A of hypothese B de beste verklaring is voor een fenomeen, hebben data alleen maar betekenis als ze onderscheidend vermogen hebben tussen beide hypotheses.
Hoewel de rol van evidence vaak benadrukt wordt (denk bijvoorbeeld aan de term evidence based medicine), hebben data op zichzelf weinig waarde. Data gaan pas leven in het licht van hypotheses, theorieën of modellen. Aangezien het verzamelen van gegevens vaak een moeizame en kostbare aangelegenheid is, is het zaak om dit zo efficiënt en doelgericht mogelijk te doen. Daarom is het zeer van belang om de vraag te stellen wat het doel is van de theorie of het model. Veelal is dat om te leren begrijpen en vervolgens te voorspellen hoe een actie (bijvoorbeeld een kracht op een onderdeel) een fenomeen beïnvloed (bijvoorbeeld de doorbuiging van het onderdeel).
Daarbij is een zeer bruikbare vuistregel om voor dat doel een parsimonious model – een eenvoudig model – te gebruiken. Dit staat bekend als Ockham’s scheermes11Occam’s razor – Encyclopedia Britannica definition. Geraadpleegd 27 oktober 2015., genoemd naar de 13e eeuwse William of Ockham. Deze vuistregel stelt dat bij concurrerende modellen of theorieën gekozen moet worden voor de eenvoudigste die past bij de data. Een reden dat deze vuistregel vaak werkt is omdat het onderscheid maakt tussen echte data en ruis die altijd in metingen aanwezig is. Waar eenvoudige modellen met name eerste orde effecten beschouwen, hebben complexere modellen de neiging om gevoeliger te zijn voor de invloed van ruis. Ondanks het feit dat dit een nuttige vuistregel is, is de keuze in de praktijk vaak niet zo eenvoudig, aangezien het nogal eens voor komt dat het ene model een betere fit met de data heeft, terwijl een ander model simpeler is. Dit op zich is al een illustratie van het feit dat de data niet op zichzelf staat en dat de beoordeling ervan samenhangt met theoretische, niet op empirische waarnemingen gebaseerde collectieve en individuele achtergrondkennis.
Logica
De derde component van het PEL-model is logica. Logica is het gereedschap om connecties te maken tussen bouwblokken zoals data, theorie, modellen, voorspellingen en conclusies. Hierbij kan onderscheid gemaakt worden in twee verschillende methodes: deductieve en inductieve logica. Bij deductieve logica – ook wel formele logica – zit de conclusie al vervat in de uitgangspunten. Neem bijvoorbeeld de uitgangspunten: (I) elk zoogdier heeft een hart, en (II) elke muis is een zoogdier. Daaruit kan de conclusie worden getrokken dat elke muis een hart heeft. Als de uitgangspunten waar zijn, dan kan bij deductie met zekerheid worden gesteld dat de conclusie waar is. Bij inductie is dat echter niet het geval. Inductieve logica voegt informatie toe die niet in de uitgangspunten gevat zit. Bijvoorbeeld: uit het uitgangspunt elke muis die ooit geobserveerd is heeft een hart, zou de conclusie getrokken kunnen worden elke muis heeft een hart. Maar of dit waar is, is niet zeker. Bij inductie kan op zijn best een grote mate van waarschijnlijkheid worden bereikt, maar nooit logische ware conclusies. Daarbij geldt: de conclusie is sterk als de uitgangspunten theoretisch of empirisch sterk zijn. Deze verschillen tussen beiden soorten logica komen ook tot uiting in toepassing ervan. Deductieve logica werkt van algemeen naar specifiek12deductive – definition in Oxford dictionary. Geraadpleegd 25 oktober 2015. In de praktijk betekent dat veelal dat er met een algemeen model een specifieke voorspelling wordt gedaan. Bij inductie geldt het omgekeerde: uit specifieke gegevens wordt een algemeen model afgeleid13inductive – definition in Oxford dictionary. Geraadpleegd 25 oktober 2015.
Het belangrijkste aspect van deductie is dat hiervoor een systeem van regels (axioma’s) kan worden opgesteld en dat als die gevolgd worden er logisch correcte conclusies worden bereikt. Ook bij inductie zijn er regels van toepassing (zoals Kolmogorov’s axioma’s14Shafer, G., & Vovk, V. (2006). The Sources of Kolmogorov’s Grundbegriffe. Statistical Science, 21(1), 70–98. en waarschijnlijkheidsleer), maar in tegenstelling tot deductie zijn er er ook twee vooronderstellingen nodig. Ten eerste werkt inductie alleen als wordt aangenomen dat de wereld uniform en regelmatig van aard is. Ten tweede moet worden voorondersteld dat de wereld is in te delen in een eindig aantal verschillende zaken of, anders gezegd, dat er klasses te zijn onderscheiden met dezelfde relevante eigenschappen6. Stel dat in autopsiemonsters van menselijk hersenweefsel lymfevaten worden aangetroffen15Louveau, A., et al. (2015). Structural and functional features of central nervous system lymphatic vessels. Nature, 523(7560), 337–341.. Een inductieve redenering die stelt dat dit bij alle mensen het geval is, vooronderstelt dan dat (I) er uniformiteit is waardoor een meting die op een andere dag of plaats gedaan wordt niet ineens anders is, en (II) dat mensen in een klasse vallen met vrijwel dezelfde anatomie.
Je kan je afvragen waarom wetenschap gebruikt maakt van inductieve logica als die zo duidelijk ruimte laat voor onzekerheden. Bovenstaande lymfevaten-voorbeeld illustreert goed wat hiervoor de reden is: zonder inductie zou het onmogelijk zijn om algemene toepasbare inzichten te krijgen en zou de observatie alleen van toepassing zijn op de individuen waarvan autopsiemonsters zijn onderzocht.
Bij zowel deductieve als inductieve logica worden regelmatig fouten gemaakt die logical fallacies worden genoemd. De ruimte is hier te beperkt om ze allemaal te bespreken, maar er zijn hele websites aan gewijd16LogicalFallacies.info. Geraadpleegd 27 oktober 2015. Daarnaast worden termen als p-waarde en significant, afkomstig uit de frequentistische waarschijnlijkheidsleer, vaak onjuist geïnterpreteerd17Goodman, S. (2008). A Dirty Dozen: Twelve P-Value Misconceptions. Seminars in Hematology, 45(3), 135–140.. Aangezien ze veel worden gebruikt in voedings- en medisch onderzoek, is goed begrip ervan belangrijk. De belangrijkste punten zijn daarbij dat de p-waarde geen uitspraak doet over de kans dat de onderzochte hypothese waar is18De betekenis van de p-waarde is: de kans om, aangenomen dat de nulhypothese waar is, data te vinden die even extreem of extremer is dan de geobserveerde data (in symbolen: P(D|H0)). Dit wordt significant genoemd als die kans kleiner is dan 5%. De p-waarde zegt echter niets over de kans dat de nulhypothese waar is bij de gevonden data (P(H0|D)) en dus ook niets over de kans dat de hypothese waar is., en dat een significant resultaat niet betekent dat het effect groot is, noch dat het aangetoond is19Een significant resultaat betekent bij placebo-gecontroleerd onderzoek dus dat, gegeven dat het medicijn niet beter is dan de placebo, de kans op een resultaat dat even extreem of extremer is dan het gevonden resultaat, kleiner is dan 5%. Anders gezegd, het is de kans dat je net zo’n extreme verdeling van het aantal genezen personen vind tussen de twee groepen (bijvoorbeeld 30 op de 100 in de placebogroep en 50 op de 100 in de ‘actieve’ groep), terwijl beide groepen een placebo kregen. De p-waarde betekent dus niet dat de kans dat het medicijn niet beter is dan de placebo kleiner dan 5% is. Ofwel, het vertelt ons dus niet hoe groot de kans is dat deze verdeling aan genezingen tussen de groepen komt doordat het medicijn werkt..
Verwevenheid
In voorgaande tekst heb ik de basiselementen van de wetenschappelijke methode doorgenomen: vooronderstellingen, aanwijzingen, deductieve en inductieve logica. Onderwijl kwamen termen zoals modellen, hypotheses, theorieën, en metingen voorbij. Ook die zijn onderdeel van de wetenschappelijke gereedschapskist. Tezamen met specialistische methoden en technieken – zoals deeltjesversnellers, vragenlijsten, of DNA-sequencing – zijn dit de methoden die gebruikt worden om wetenschap te bedrijven.
Ze bieden een methodologisch zeer robuuste manier van kennisvergaring en -groei. Hoewel het niet de enige methode is, is het de sterkste die we kennen. Toch maakt het gebruik van de wetenschappelijke methode de gevonden resultaten nog niet wetenschappelijk bewezen. Eén resultaat of één onderzoek betekent namelijk weinig. Het is de coherente samenhang met andere theorieën en resultaten die de mate van geloofwaardigheid bepaalt20Kosso, P. (2008). The Large-scale Structure of Scientific Method. Science & Education, 18(1), 33–42.. Daarin schuilt de essentie van het begrip kennis.
Neem een simpele digitale keukenweegschaal. Het ding lijkt weinig spannend en niemand zal zijn werking in twijfel trekken. Maar de totstandkoming ervan leunt zwaar op wetenschappelijke kennis. Op Newton’s tweede wet, op inzichten over zwaartekracht, op ontdekking van piëzo-elektrische materialen, op de wetten van Ohm en Kirchhoff, en zelfs op fundamenteel begrip van getallen. Al deze en andere kennis die in je simpele keukenweegschaal wordt toegepast, bestond niet zo lang geleden nog niet. Stuk voor stuk begonnen ook deze concepten als een theorie en enkele observaties. Wat heeft er nu voor gezorgd dat deze concepten bewezen worden geacht, of beter nog als volkomen geaccepteerde kennis, zelfs als natuurkundige wet? Het antwoord is het netwerk van onderzoek en theorieën. Elk van deze zaken is op tal van verschillende manieren onderzocht, met verschillende meetprincipes en een groot scala aan testen. Zo is Newton’s tweede wet niet alleen onderzocht met een vallende kogel of appel, maar ook door de bewegingen van hemellichamen zoals de maan te bestuderen. Ook is er samenhang tussen Newton’s tweede wet zijn zwaartekrachtswet, maar ook met de speciale en de algemene relativiteitstheorie van Einstein, die elk weer hun eigen evidence kennen.
Bovenstaande beschrijving illustreert nog iets essentieels. Want meetapparatuur zoals een weegschaal en de bijbehorende wetenschappelijke kennis worden nu gezien als betrouwbare middelen. Ze worden in onderzoek gebruikt om evidence te leveren voor geheel nieuwe theorieën en staan zelf niet meer ter discussie. Denk bijvoorbeeld aan onderzoek naar overgewicht, waarin de weegschaal slechts een (vaak niet eens benoemde) tool is. Wetenschap is geen los onderzoek, het is een verweven netwerk waarin nieuwe concepten op goed ondersteunde oude voortbouwen. Het is die coherentie die van een hypothese een bewezen concept kan maken. De coherentie tussen verschillende soorten testen, maar ook tussen theorie en data, tussen theorie en theorie. En tussen theorie en vooronderstellingen.
‘Bewezen’ = coherentie met bestaande kennis
Wat bewijs is, staat in feite in de vorige alinea. De mate van geloofwaardigheid van een theorie of resultaat wordt bepaald door de coherentie met bestaande kennis. Dat betekent iets heel wezenlijks, namelijk dat één test, hoe groot de uitslag ook moge zijn, nog géén bewijs is. Het is slechts evidence. Ook herhaling van de proef maakt hier nog geen sterk bewijs van (alhoewel de aannemelijkheid er wel door zal groeien). Pas als er verwevenheid ontstaat, door evidence uit diverse andere typen onderzoek en door samenhang met theoretische modellen, pas dan kan worden gesproken van bewezen en wordt een concept onderdeel van onze gezamenlijke kennis. Helaas is dit in de wereld van modern voedingsonderzoek schaars. In deel twee van dit drieluik hierover meer.
Notes






